Minimum Expression and Column Subset in Subselects

Oxla's query execution engine is made up of processors connected in a pipeline. Each processor takes an input batch from its preceding processor and computes an output batch for its following processor in the pipeline. Batch is a container for columns. For simplicity, let us assume that each processor computes a set of new expressions (Expr) stored in the output batch. Each expression depends on a subset of columns (Cols) located in the input batch. The size of batches (number of columns in the batch) passed between processors plays a crucial role in performance and memory utilization. As you can imagine – for the world’s fastest-distributed database – achieving and maintaining exceptional performance is one of the key goals.

To illustrate the above, let us have a simple example: nested SELECT with WHERE on table T made up of one column c.

select f1,f2 ,..., fn where fn > 0 from 
  (select F1(c) as f1,..., Fn(c) as fn where c > 0  from T)

The execution pipeline for the above SQL query consists of two filter processors, P1 and P2. Processor P1 computes the results of inner select, filters rows (c>0), and creates input for the P2 processor that computes the final result. Without any optimization, P1 computes a batch made up of n columns (f₁, …, f_n) that will be consumed by P2. Processor P2 filters rows (fn > 0) and returns the final batch. We can see that columns (f₁, …, f_n) are copied 2 times in P1 and P2. However, if we choose the optimal subset of expressions and columns for P1, we will return just one column c, and evaluation of all expressions (f₁, …, f_n) will be delayed. This solution is valid because all columns (f₁, …, f_n) can be computed based on c when needed, so we do not lose any expression. Next, P2 will compute the final columns (f₁, …, f_n) based on the c column and build the final output batch. This way, we avoid the copy operation of (n-1) columns in the P1 processor. Of course, we could use other optimizations here, like flattening of our select. However, such optimizations are not possible when dealing with joins, as we will see in the next example. Let us observe that a returned subset of expressions and columns must be valid; that is, all delayed expressions must be computable from a returned subset of columns.

Naive min-heuristic

We could try to use a naive min-heuristic: if |Expr| < |Cols|, then compute and return all expressions (and all input columns can be dropped). Otherwise, return all columns and delay all expressions. Of course, the min-heuristic is valid (we can compute all delayed expressions when needed). Unfortunately, this heuristic may behave very inefficiently. Let us consider an example: we have got set of n expressions to compute Expr = {v₁ , …., v_n} and a set of n input columns Cols = {u₁, …., u_n}. Now, first, n-1 expressions {v₁ , …., v_n-1} depend on the last column u_n only, and the last expression v_n depends on all columns. The following bipartite B=(Expr, Cols) graph shows dependencies between expressions and columns (figure 1).

If we apply our min-heuristic, then we always return n columns (either all expressions or all columns) in the output batch. However, the optimal solution requires only two output columns in total: one expression {v_n} and one column {u_n}. This solution is valid since all delayed expressions {v₁, … , v_n-1} can be computed based on u_n, and all columns {v₁, … ,v_n-1} can be safely dropped since only expression v_n required them.

Let us have a closer look and see what impact optimal expressions and columns selection may have on SQL query with joins. Consider the two-level join on T1, T3 made up of n + 1 int columns (u₁, … , u_n, c₁) and T2,T4 made up of just one column c1. The dependencies between expressions and columns in both subselects are represented by figure 1.

select f1, ..., fn , g1, ..., gn  from 
  (select f_1(Un) as f1, ... , f_n-1(Un) as f_n-1, f_n(U1, ..., Un) as fn, c1 from T1 JOIN T2 ON T1.c1 = T2.c2) as L 
  JOIN 
  (select g_1(Un) as g1, ... , g_n-1(Un) as g_n-1, g_n(U1, ..., Un) as gn, c1 from T3 JOIN T4 ON T3.c1 = T4.c1) as R
  ON L.f_n = R.g_n

Our select execution pipeline is made up of two nested join processors (L for T1 and T2, R for T3 and T4) and a final join processor for L and R subselects. If we use the min-heuristic, then both nested join processors L and R will read columns T1(u₁, … , u_n, c₁), T2(c1) and T3(u₁, … , u_n, c₁), T4(c1), respectively. Next, both processors, L and R, will create an output batch of the same shape with columns (f₁, … , f_n) and (g₁, … , g_n), respectively, input for the final join processor. We can see that columns (f₁, … , f_n) were copied two times (in L processor and final join processor); the same happens with (g₁, … , g_n). If we select an optimal subset of expressions and columns in L and R processor, which is (f_n , u_n) and (g_n,u_n), respectively, then the nested join processors will return just two columns, and the final join processor will compute output batch of with columns (f₁, … , f_n, g₁, … , g_n). This way we can save on copying (n-2) columns in each of our nested join processors.

Formal problem definition and our results

In this article, we present a polynomial time algorithm that computes a minimum valid subset of expressions and columns. Let us call our problem "Minimum Expression and Column Subset" (MECS) and formulate it in graph theory terms; MECS(Expr, Cols, B):

• ‍Input: set of expressions Expr and set of columns Cols that create bipartite graph B=(Expr, Cols, E), edge (v,u) belongs to set of edges E if column u in Cols is an input for expression v in Expr.‍
• Output: Valid subset ExprE (Expressions to Evaluate) and subset ColsM (columns to Move) that minimize the total number of columns returned |ExprE| + |ColsM|.

The above problem can also be used in compression problems where we want to store a minimum number of columns |ExprE| + |ColsM| (optimize memory) so that all expressions in Expr can be computed when needed.

To show a relationship between the max matching problem and “Minimum Expression and Column subset”, we will need Hall’s theorem.

‍
Hall’s Theorem:Let G = ( X, Y, E ) be a finite bipartite graph with bipartite sets X and Y and edge set E. An X-perfect matching (also called an X-saturating matching) is a set of disjoint edges, which covers every vertex in X. For a subset W of X, let N ( W ) denote the neighborhood of W in G, the set of all vertices in Y that are adjacent to at least one element of W. The marriage theorem in this formulation states that there is an X-perfect matching iff for every subset W of X | W | ≤ | N ( W ) | . In other words, every subset W of X must have enough neighbors in Y.

‍

Theorem 1:
Optimal valid solution (OptSol) of the MECS(Expr, Cols, B) problem, made up of sets ExprE (expressions to evaluate a subset of Expr) and ColsM (columns to move a subset of Cols), induces max matching in bipartite graph B=(Expr, Cols, E). The size of the max matching is |ExprE| + |ColsM|, all nodes in ExprE and in ColsM belong to the matching (see figure 2).

‍

Proof:
Let us assume that we have an optimal valid solution, OptSol.
OptSol partitions set Expr into two subsets:

• ExprE – set of expressions to evaluate
• ExprD – set of expressions to be delayed

and set of Cols into two subsets:

• ColsM – set of columns to be moved
• ColsD – set of columns to be dropped.

Observations:

1. We cannot have any edges between nodes in ExprD and ColsD. This is because the solution must be valid. No delayed expression in ExprD can depend on a dropped column in ColsD.
2. We may have edges between ExprE and ColsM; ExprE and ColsD; ExprD and ColsM

Lemma 1‍

A matching of size |ExprE| exists between each expression node in ExprE and ColsD.

Proof:

By Hall’s theorem, we need to show that each subset X of ExprE has at least |X| neighbors in ColsD.
So, let us assume the contrary that we do not have matching in which every node in ExprE is matched with some node in ColsD. This implies that we have a subset X of nodes in ExprE that is mapped to a subset of nodes Y in ColsD such that |X| > |Y|. However, this implies that we could find even more optimal solution to our problem by merging X into ExprD and Y into ColsM. This operation results in a valid solution lower than our original solution by |X| - |Y| (see figure 3). This contradicts our assumption that our solution, OptSol, is optimal.

Lemma 2

‍There exists a matching of size |ColsM| between each column node in ColsM and ExprD.

Proof

By Hall’s theorem similar to Lemma 1.

‍
Next, we will show that matching from Lemma 1 merged with matching from Lemma 2 must be max matching (MM) in graph B.

Lemma 3‍

MM matching of size |ColsM| + |ExprE| is max matching in B.
‍Proof:

Let us observe that any other maximal matching would have to contain edge between node v in ExprE and node w in ColsM. This is the only possibility since we do not have any edges between ExprD and ColsD due to the validity property. However, we can see that such matching is lower by one edge than MM since two edges from MM (adjacent to v and w) would have to be removed and replaced by a new edge (v,w).

By Lemma 1 and Lemma 2 we can match all nodes in ExprE with nodes in ColsD and all nodes in ColM with nodes in ExprD. By lemma3 this must be max matching.

□

Theorem 2:
We can compute a solution at most twice larger than the optimal solution in polynomial time.

Proof:
Compute max matching MM.
Each matched expression will belong to the ExprE. Each column that is matched will belong to the ColM. Observe that we do not have any edges between ExprD and ColD since MM is max matching (otherwise, we could construct even larger matching). So, such a solution is valid. By theorem 1, the optimal solution induces max matching where half of the nodes in the max-matching belong to the optimal solution. Since we do not know yet how to compute the proper half of the nodes in matching that make up the optimal solution, we include all expression nodes in the max matching into ExprE, and their matched columns are included into ColsM as well. So, our solution is at most twice larger than the optimal solution.

□

The next theorem will show us how to compute optimal solutions based on max-matching.

Theorem 3:
Max matching computed for B=(Expr, Cols, E) can be converted to an optimal valid solution in polynomial time.

‍
Proof:‍

Compute max matching MM in B. Initialize ExprE, ExprD, ColsD, ColsM in the following way.

1. All expressions in matching MM belong to ExprE (expressions evaluated).
2. All expressions that not in match MM belong to ExprD (expressions delayed).
3. All cols in matching MM belong to ColsD (columns dropped).
4. All cols not in match MM belong to ColsD (columns dropped) as well.
5. Initially, ColsM (columns moved) is empty.
   

Of course, such a solution may not be valid due to edges between ExprD and ColsD, so we need to fix it in the fixing loop.

while (exists edge (v,u) between v in ExprD and u in ColsD – the solution is not valid)
  1. Move M(u) from ExprE to ExprD. Where M(u) is the expression matched with col u in matching MM
     (in lemma 4, we will show that M(u) must always be correctly defined).
  2. Move u from ColsD to ColsM.

Lemma 4

‍When executing the fixing loop M(u) is always well defined.

Proof: ‍

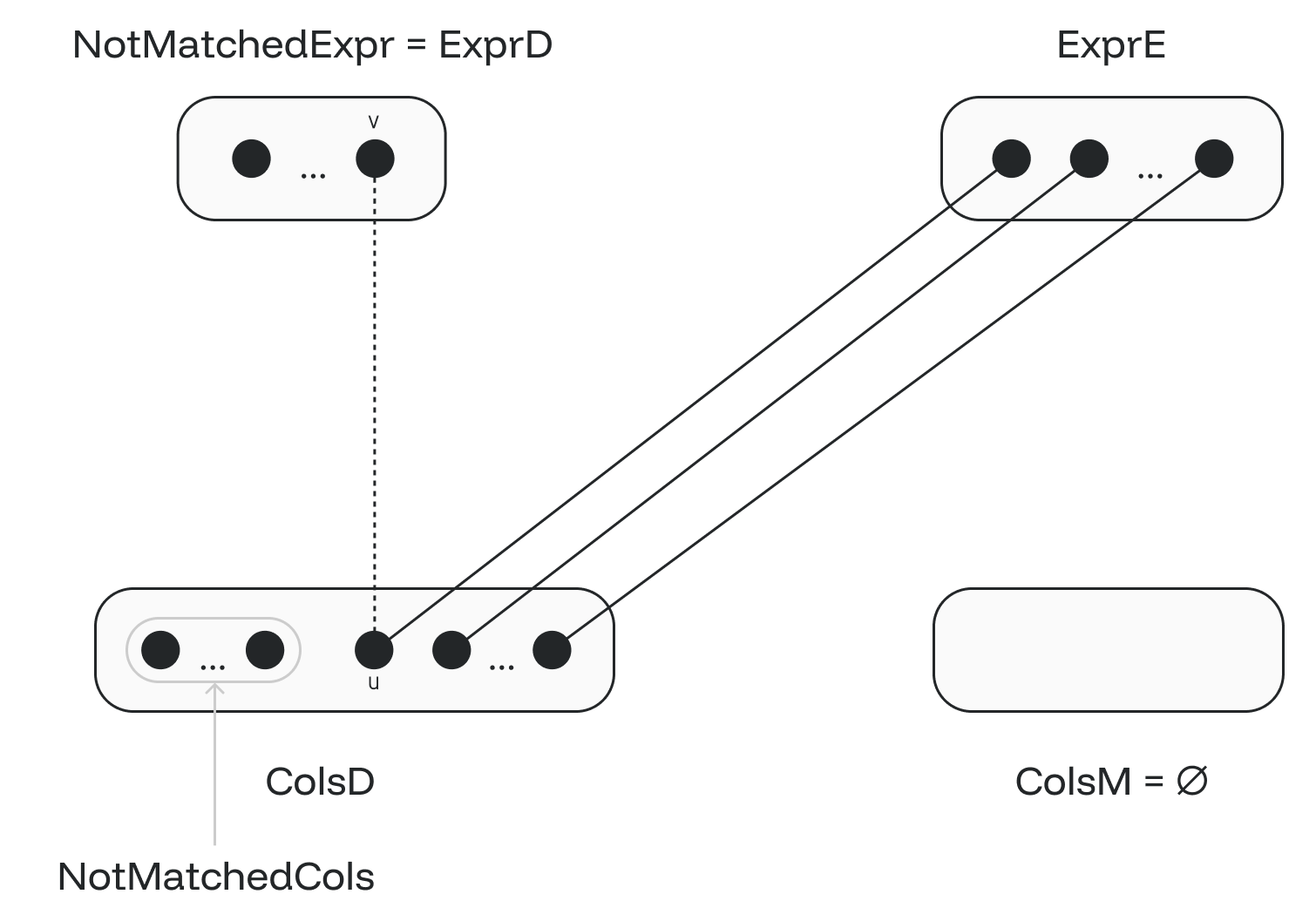
Let’s call expressions not in match MM NotMatchedExpr. Initially, NotMatchedExpr set is equal to ExprD set. Let’s call columns not in match MM NotMatchedCols. Initially, NotMatchedCols set is a subset of ColsD set. Observe that:

1. We do not have any edges between NotMatchedExpr and NotMatchedCols (figure 4). If we had such an edge (v,u), we could construct an even larger matching by including edge (v,u) into our max matching MM. So, initially, we can only have edges (v,u), where v is in NotMatchedExpr and u in (ColsD – NotMatchedCols).

2. When moving M(u) from ExprE to ExprD, we cannot have any edge joining M(u) to any node in NotMatchedCols. Let us consider the initial state when fixing the first invalid edge (v,u).
Let’s assume that an invalid edge (M(u),w) (where w is in NotMatchedCols subset) is created when moving M(u) to ExprD and u to ColsM. In such a case, our fixing loop would not fix (M(u), w) since M(w) is not defined. Observe that the existence of (M(u), w) edge allows us to build even larger matching by removing (u, M(u)) and including (v,u) and (M(u), w) (see figure 5) contradicting maximality of matching MM.

In a more general case, after a few expression nodes m was moved to the ExprD from ExprE in the process of fixing invalid edges, then if there was an edge in (M(u),w) when fixing m+1 invalid edge (v,u) then we could create new matching by removing (M(u), u) and including (M(u), w) and (v,u). if v is matched with some col node w1 in ColsM then we remove (v,w₁) and include (w₁,v₁). Edge (v₁,w₁) must exist since w₁ was moved to ColsM before due to an invalid edge (v₁,w₁). V₁ could be matched with w₂ in such case we remove (v₁,w₂) and include (w₂, v₂). (w₂, v₂) must exists since w₂ was moved due to invalid edge (w₂,v₂). We continued this process until we hit column node w_k (w3 on figure 6), which was fixed due invalid edge (v_k, w_k) where v_k in NotMachedExpr. So, we can safely include (v_k, w_k) to the new matching as the last edge. In the worst case, edge (v_k, w_k) will be the first invalid edge that was fixed. New matching is by one edge larger than our original matching MM, contradicting the maximality of MM. In figure 6, we’ve included dashed edges (5 edges) to the new larger matching and removed solid edges (4 edges) from MM matching.

The presented algorithm works in the polynomial time: computing max matching O(|V| * |E|) and fixing loop requires O(|V| + |E|). As an exercise, we leave the application of this algorithm to the graph presented in the first figure.

If you're curious about the intricacies of Oxla's query execution engine and want to dive deeper into its features, the Oxla BETA is now available for free to deploy in just 2 minutes. Dive into the experience, and don't hesitate to drop your thoughts and feedback to hello@oxla.com.

Thanks, Wojciech Oziebly and Grzegorz Dudek, for your valuable algorithmic insights!